Im Zuge des Themas „Lineare Gleichungen“ wurde zunächst die Basis erarbeitet: Die Klasse sich zunächst mit der Bedeutung und Funktion von Variablen auseinandergesetzt. Anschließend erfolgte eine Unterscheidung von Term, Funktion und Gleichung. Hierbei wurde auch das Ausmultiplizieren wiederholt und das Zusammenfassen geübt. Das Umformen von Gleichungen wurde gemeinsam mit dem „Waage-Modell“ erarbeitet, um den Schülerinnen und Schülern eine visuelle Brücke zu den Äquivalenzumformungen zu bauen. Diese wurden gemeinsam Erarbeitet und eingeübt.
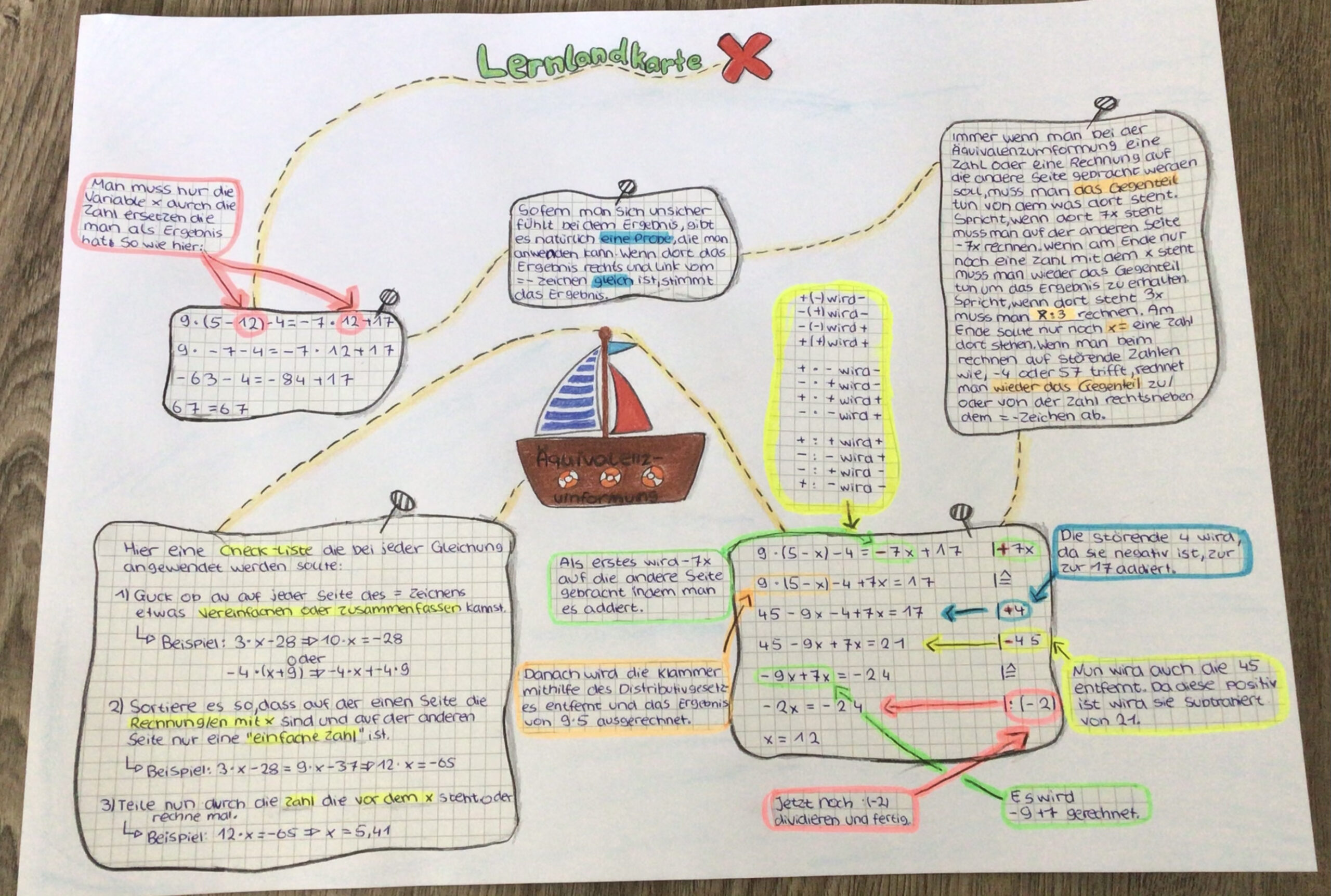
Um das erarbeitete Wissen der Klasse zu überprüfen erfolgte nun die Erstellung einer Lernlandkarte anhand individueller Gleichungen – jedes Klassenmitglied erhielt eine eigene, lineare Gleichung. Dabei sind die Gleichungen so gewählt, dass die zuvor erarbeiten Unterthemen (Ausmultiplizieren, Umformen von Zahlen sowie Zahl-Variabeln und Vereinfachen/Zusammenfassen) zum Lösen angewendet werden müssen. Um den SuS eine gewisse Sicherheit zu geben, wurden die Lösungen der Gleichungen so gewählt, dass sie aus ganzen, maximal zweistellige Zahlen bestehen.
Da eine Lernlandkarte nicht nur ein einfaches Aufschreiben einer Lösung zu einer linearen Gleichung darstellt, sondern eine Visualisierungsmethode, mit der das Gelernte bildlich veranschaulicht und verknüpft wird, stellte diese Leistung den Schwerpunkt in der Bewertung dar.

Als Produkte sind ganz unterschiedliche Darstellungsvarianten entstanden. In einem Peer-Feedback konnten die Schülerinnen und Schüler gegenseitige Arbeiten einsehen und andere Ausführungen erleben. Einige Beispiel zu den Lernprodukten sind anbei aufgeführt.
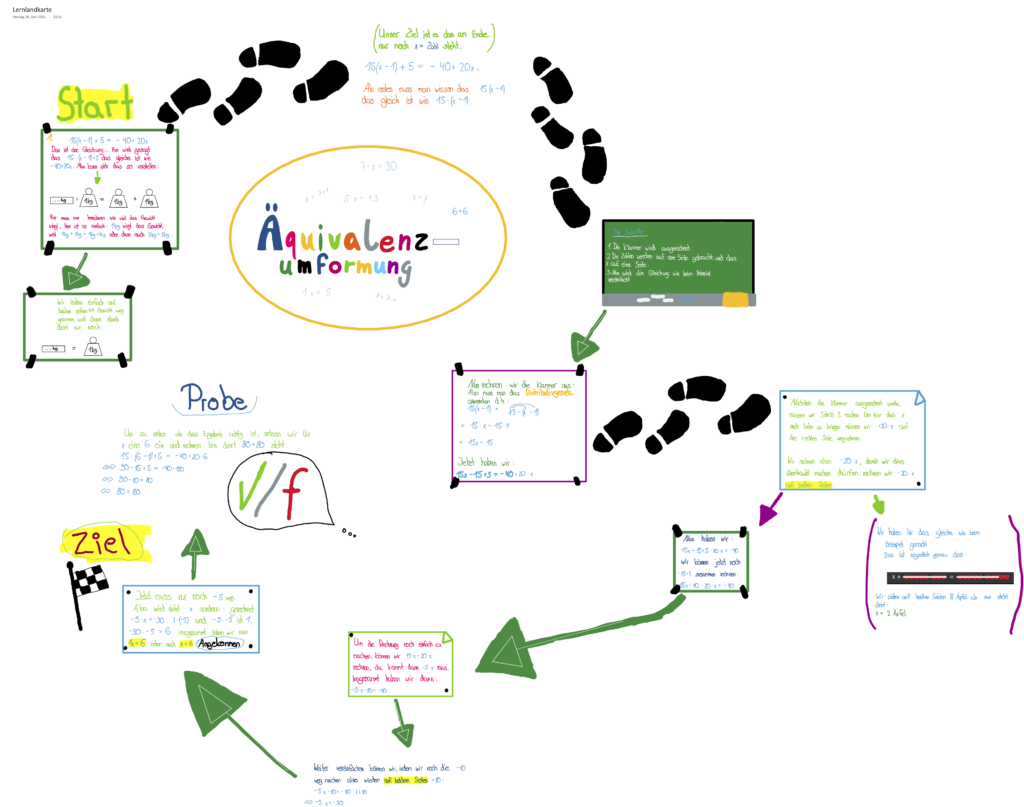
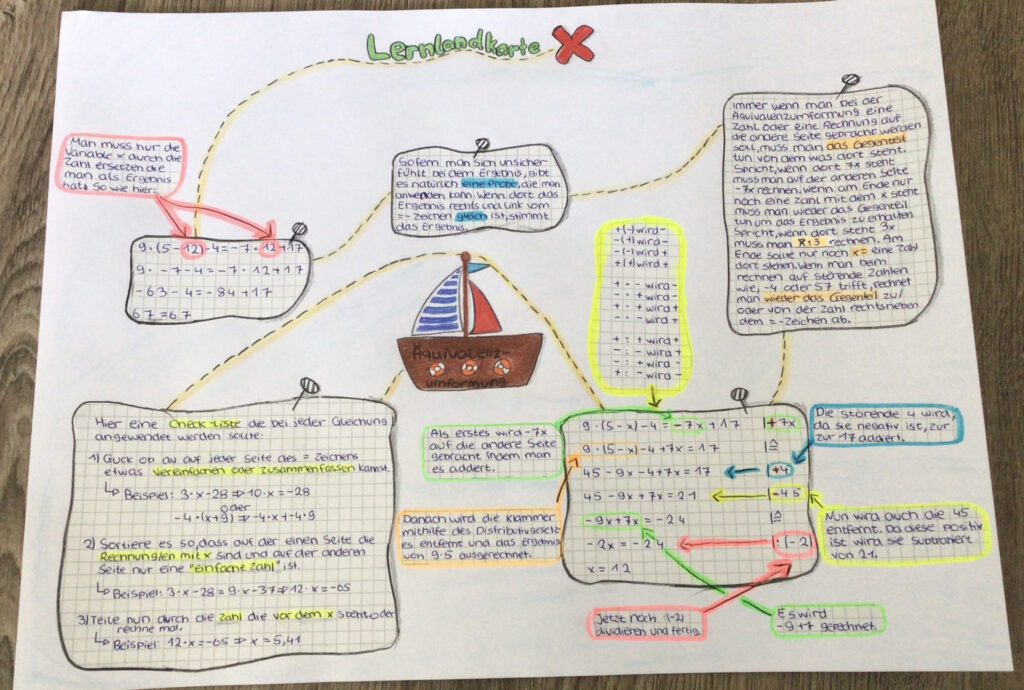
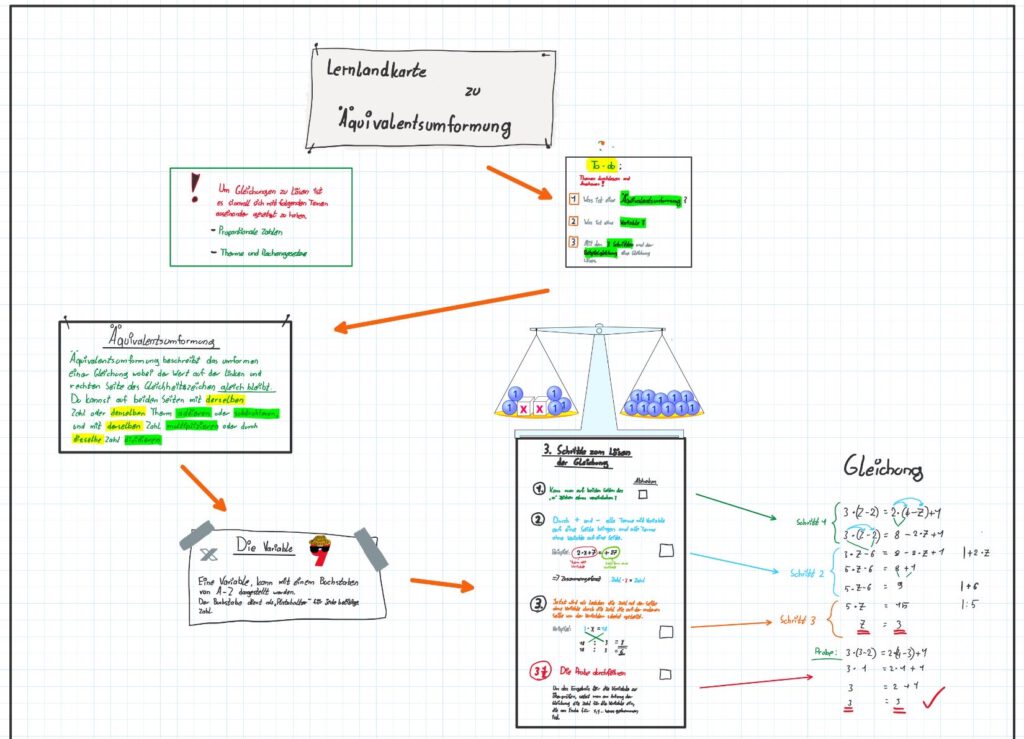
Zur Ermittlung der Bewertung wurden die in der Übersicht genannten Aspekte beurteilt. Hierbei war, wie bereits genannt, die Übertragung des erworbenen Wissens in eine Lernlandkarte Schwerpunkt der Leistung.

Schreibe einen Kommentar